Fusion of mathematics and material science allows for accurate prediction of graphene catalysts using mathematical model

A research group that included Professor Motoko Kotani and others from the Tohoku University Advanced Institute for Materials Research developed a mathematical model that allows for design and mapping of the changes that occur when the structure of carbon-based, non-noble-metal-free catalysts are changed in certain ways. The developed method is 1 billion times faster than the conventional mapping method.

When a carbon network that was designed by this method was evaluated, it exhibited the predicted catalytic ability, demonstrating the usefulness of mathematics-based material design. Professor Kotani said, "The most important thing in materials science is the relationship between structure and function. By providing a descriptor that expresses chemical structure using mathematical (geometric) terms, we aim to provide the first guidelines for predicting and designing chemical structures that exhibit desired functions." The results of the study were published online in the journal Carbon.

In order to use three-dimensional graphene as a catalyst, it is important to understand both the precise control of the material's structure, which becomes the site of the chemical reaction, at the atomic level and the stability of the entire three-dimensional network structure. In the study of chemical reactions, it is common to simulate populations of only 300-1000 atoms, owing to the constraints of computational resources. However, this makes it difficult to accurately understand the properties of the entire material, so the stability of the entire structure can only be inferred from the local structure. Therefore, catalyst design has relied heavily on experience and intuition to identify, by trial and error, the best solution from among a huge number of options.

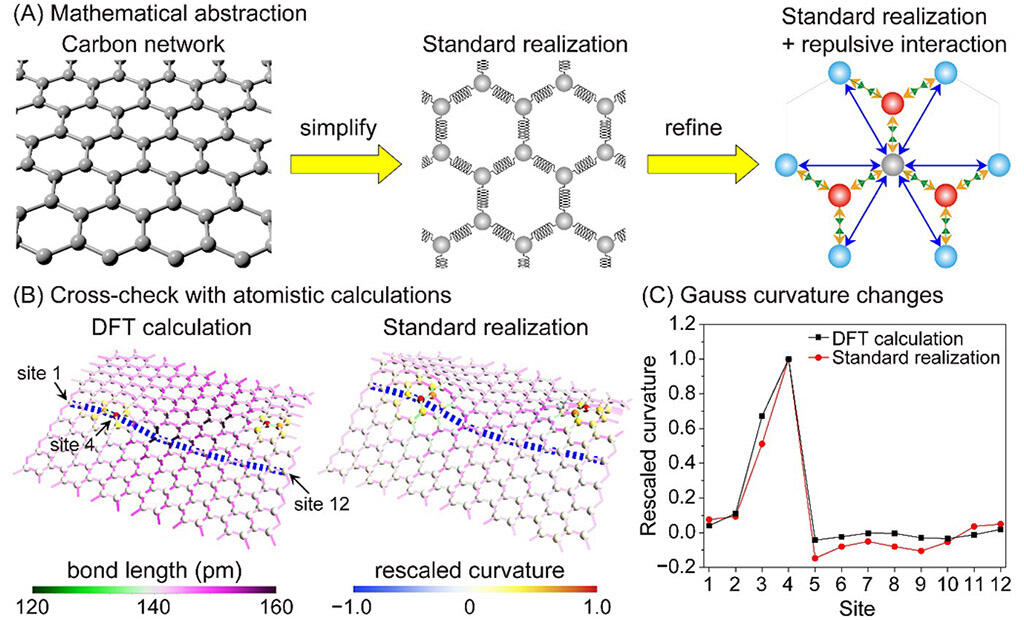
The research group applied a mathematical model (standard realization using Gaussian curvature), which is used to determine the distance between two points on a curved surface, to a carbon network in order to evaluate the internal strain of the structure and to quantify the chemical reaction field's geometric structure. In order to reproduce an accurate structure, the group developed an improved standard realization model that incorporated the minimum necessary physical phenomena by considering the repulsive force between neighboring atoms. Use of the improved model revealed that the structure of a graphene lattice of six-membered rings that contained defects (paired five- and seven-membered rings) were almost identical to that reproduced using ab initio* calculations. A simple comparison of calculation time with one CPU core indicated that the calculation time for the improved standard realization was 39 microseconds, whereas that for the ab initio calculation was 46,000 seconds. In other words, the new model accelerated the calculation by 1 billion times.

In order to impart catalytic ability to graphene, one carbon atom and one nitrogen atom of graphene with 5/7-pair defects were replaced at various sites. Detailed analysis of the deformed structure revealed that the structural features of the ab initio and improved standard calculations were nearly identical. The research also revealed that changes in Gaussian curvature were dependent on the position of replacement. In order to give Gaussian curvature a physical meaning, the ease of replacement with nitrogen at each location was quantitatively estimated by the physical quantity of energy using ab initio calculations. This revealed that the energy needed to exchange nitrogen was small where the change in Gaussian curvature was large and large where the change in Gaussian curvature was small.

The ease of nitrogen doping, which determines the catalytic ability of the material, can be quantified using the Gaussian curvature that describes the local structure. It is possible that structural defects must exist in order to form curved surfaces, and different elements can be introduced to stabilize the structure (i.e., Gaussian curvature approaches zero) and to eliminate geometric strain (i.e., high Gaussian curvature) on the five-membered ring of defects. In contrast, if a substance is designed so that the Gaussian curvature of the doping region is high, then the target substance can be introduced there. In order to demonstrate the results of these simulations, three-dimensional nitrogen-sulfur-doped graphene was prepared, and a large amount of nitrogen and sulfur were introduced around the 5/7-pair defect. Scanning electrochemical cell microscopy revealed that a curved surface with multiple defective structures had a greater capacity for catalyzing hydrogen generation than a flat surface.

and molecular structures using quantum mechanics, without experimental data.

This work demonstrates Gaussian curvature is effective for the catalyst design of the carbon network. However, the search for connections between mathematical parameters and physical and chemical parameters has just begun. The improved standard implementation method can be used to calculate a model of infinite size in principle, and complementary combination with existing simulations enables large-scale calculations for carbon networks with more than 10,000 atoms.

Professor Kotani said, "In this study, we incorporated the relationship between catalytic activity (function) and curvature (geometry) into the design, but other related research, such as investigations of structural stability against tensile strength in elastomers, is also is underway. We hope that using more intuitive descriptors in machine learning will deepen our understanding of the phenomenon."

* Ab initio is a calculation used to calculate atomic