Water droplets in liquid: straight to curvilinear movement transition

A research group including Kyoto University Graduate School of Science graduate student Saori Suda (at the time of research) and lecturer Masatoshi Ichikawa; Keio University JSPS Research Fellow Tomoharu Suda, and Max Planck Institute for Terrestrial Microbiology HFSP Fellow Takuya Ohmura, conducted experiments and theoretical calculations to observe the movement of water droplets in a liquid and found that as the water droplet increased in size, it stopped linear movement and began to 'wander around' its environment.

Water droplets were known to exhibit a variety of movements when swimming in liquids; however, until now, it was not clearly understood how these movements were triggered. According to Dr. Ichikawa, "We were interested in spontaneously moving objects, which are universal to both living and non-living objects. Focusing on self-propelled droplets made of water, oil, and surfactant, we conducted an experiment to investigate spontaneous changes of motion."

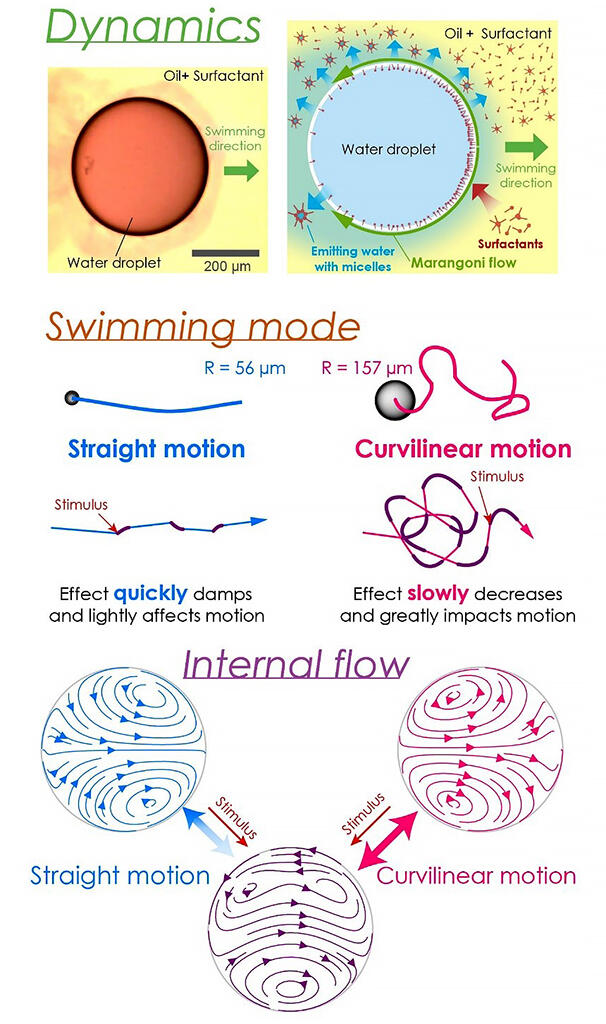
In the experiment, the group observed a simple self-propelled system consisting of pure water droplets, oil, and a surfactant. First, through observation using a microscope and precisely controlling the size of the water droplet, it was found that when the water droplet is enlarged, its motion changes from straight-line motion to curvilinear movement.

Next, to investigate the cause of this change, particle image velocimetry (PIV), which measures convection, was used to measure the internal convection pattern of water droplets near a radius of 100 micrometers where the change in movement occurs. It was found that the gradient difference between the dipolar flow and the quadrupolar flow of internal convection is systematically correlated with the change in the direction of movement of the water droplets.

From this, a hydrodynamic model was created to clarify the mechanism of change in the direction of motion. If the internal convection of water droplets and the concentration of surfactant are expressed by using spherical harmonics, they can be separated into components with different symmetries. The concentration distribution of the surfactant is obtained from the advection-diffusion equation. Focusing on the fact that internal convection satisfies the Stokes equation, a differential equation expressing the interaction between the components can be obtained. The theoretically derived stability and expected behavior were compared with those under the experimental conditions; the results showed that (1) on the time scale of the experiment, the stability of a large water droplet partially changed, and that (2) large droplets exhibited a greater change in the direction of travel in response to external force and fluctuation than small droplets did.

According to Lecturer Ichikawa, "This research reveals a part of the mechanism of spontaneous movement expressed by abiotic components that resembles living things. In the future, we would like to clarify the connection between the various movements that organisms and cells show and the spontaneous movements of abiotic components."

■ Advection-diffusion equation: An equation that expresses the movement of matter in a fluid, considering both transport by advection and movement by diffusion. In the study, it was used to represent changes in the concentration distribution of surfactants.

■ Stokes equation: Generally, the motion of a fluid is expressed by the Navier-Stokes equations, but this can be simplified especially when the effect of fluid viscosity is large; the resulting equation is called the Stokes equation. This describes the flow fields that should be considered in the study.