Deep learning is a powerful data analysis technique and one of the core technologies of modern artificial intelligence. However, compared to its great practicality, the mechanism behind its high performance is still unclear, and a theoretical explanation is needed for the future development of the technology and its safe practical use. An unsolved issue of particular importance is the problem of neural network overfitting. It has been observed experimentally that the neural networks used in deep learning have a large number of parameters and therefore a very high degree of freedom, but the phenomenon of overfitting, where the neural network is over‐fitted to the training data, does not occur. This is in stark contrast to conventional theory, which states that large numbers of parameters reduce accuracy due to overfitting, and a theory is needed to resolve this problem.
A research team led by Associate Professor Masaaki Imaizumi of the Graduate School of Arts and Sciences at the University of Tokyo and Professor Johannes Schmidt‐Hieber of the University of Twente in the Netherlands, has mathematically described the phenomenon of a neural network stagnating on an energy surface and developed a new theory that this implicit regularization prevents deep learning from overfitting. The team's research was published in the online edition of IEEE Transactions on Information Theory.
Provided by the University of Tokyo
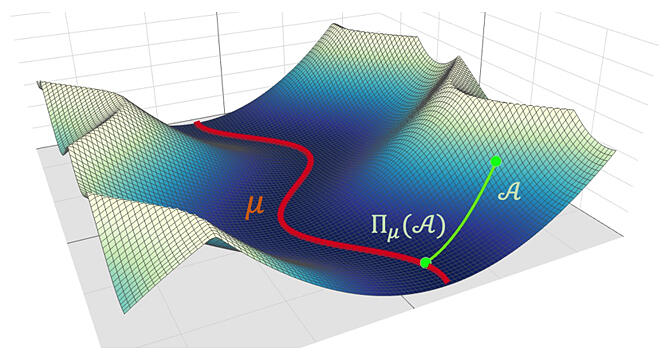
When a neural network learns, it transitions on the energy surface based on a probabilistic algorithm and searches for the optimal parameters.
The theory developed by the researchers proves that if the landscape around the local minima in this energy surface has a certain structure, the neural network will stay in this vicinity with a high probability, which is an implicit regularization that prevents overfitting in deep learning. Although a number of concrete details regarding implicit regularization have been proposed in previous theories, an effective form has yet to be formulated, with experimental counterexamples to leading hypotheses.
The present study has put forward a concrete form of implicit regularization in a mathematically valid form.
Deep learning is a data analysis technique that can achieve high performance, but its principles are still unclear, and many practical problems remain, such as high computational cost and low interpretability. The results of this research will contribute to theoretical endeavours, such as unravelling the principles of deep learning, and lead to academic developments, such as the construction of new mathematics for artificial intelligence, as well as engineering applications, such as the design of neural networks and algorithms to make learning more efficient.
Journal Information
Publication: IEEE Transactions on Information Theory
Title: On Generalization Bounds for Deep Networks Based on Loss Surface Implicit Regularization
DOI: 10.1109/TIT.2022.3215088
This article has been translated by JST with permission from The Science News Ltd. (https://sci-news.co.jp/). Unauthorized reproduction of the article and photographs is prohibited.




