Tohoku University and the University of Tokyo propose unified metric for the prediction of quantum many-body systems

The quantum many-body problem is a challenging problem. When solved, it ultimately explains phenomena occurring in the natural world by understanding and predicting new properties and phenomena of matter that arise when a large number of microscopic particles interact with each other and become intricately entangled according to the laws of quantum mechanics. It has been pointed out that quantum computers have the potential to solve quantum many-body problems with superior performance (quantum supremacy) compared to conventional computers (classical computers). However, criteria regarding the level of computation required to achieve quantum supremacy have been unclear.

Assistant Researcher Michael Schmidt of the Waseda Research Institute for Science and Engineering, Waseda University (at the time of the research), Professor Yusuke Nomura and Specially Appointed Assistant Professor Rico Pohle of the Institute for Materials Research at Tohoku University, and Professor Emeritus Masatoshi Imada of the University of Tokyo (visiting professor at Sophia University) formed an international collaboration led by PhD Student Dian Wu and Associate Professor Giuseppe Carleo of the Swiss Federal Institute of Technology Lausanne. The aim was to collect the calculation results of different state-of-the-art methods used to solve quantum many-body problems and propose a unified metric to express the accuracy of the methods.

The quantification of this accuracy has made it possible to visualize the degree of progress in numerical methods used for solving quantum many-body problems. Further, the challenges that quantum computers, which are expected to be realized in the future, must overcome are also clearly defined, along with the criteria for achieving quantum supremacy. The results are published in the online edition of Science.

To clarify the state of the art of numerical analysis methods used for solving quantum many-body problems, an international collaboration consisting of experts in quantum many-body problem analysis from various countries was formed to collect data on calculation results of various methods used to solve quantum many-body problems using classical computers.

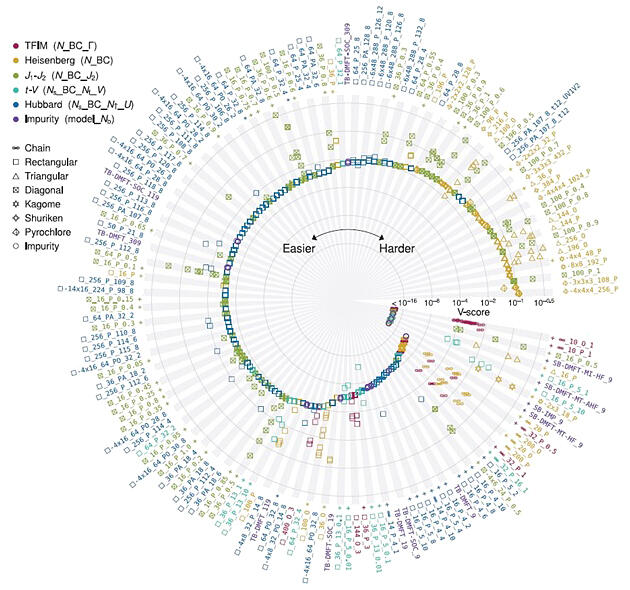
The researchers proposed a metric called V-score, which is a unified indicator of the performance of the calculation results. When a calculation is performed using a classical computer by making an approximation, it is generally not known how reliable or close the obtained answer is to the exact answer until the exact answer is determined. Further, the degree of confidence also cannot be determined until the exact answer is known. The metric V-score is the same physical quantity as the one introduced in 2000 by Masatoshi Imada—a then professor at the Institute for Solid State Physics, the University of Tokyo. This physical quantity was introduced to improve the approximation accuracy of solving quantum many-body problems leveraging the property that even if the exact answer is unknown, the exact answer is obtained when the quantity known as the dispersion of energy becomes zero. This quantity is the key to the proposed metric.

The unified performance metric V-score not only allows for a fair comparison of the performance of various numerical methods but also indicates which quantum many-body problems are difficult to solve. For example, in quantum spin systems—wherein quantum spins interact—there are problems with different properties depending on the locations of the spins and how the spins interact with each other. Among these problems, the quantum spin problem of a geometrically frustrated quantum spin system—wherein the energy gains of the spin interactions cannot be simultaneously satisfied—is particularly difficult to solve.

It was also found that problems of strongly correlated electron systems, in which electrons strongly interact with each other and travel around in a crystal, tend to be more difficult than quantum spin problems. By collecting data on various calculation results and analyzing them using the unified performance metric, the researchers succeeded in quantifying the current state-of-the-art that indicates the performance level of classical computers where they can be used to solve quantum many-body problems.

This result also clarified the criteria for the level of performance a quantum computer must achieve to realize quantum supremacy. The successful quantification of the performance of numerical analysis of quantum many-body problems provides a clearer indication of the direction in which quantum many-body computation methods should progress. From the perspective of classical computers, further advances in the methodology can further improve the metric score, allowing us to unravel the mysteries of unsolved quantum many-body problems, and for quantum computers, quantifying the performance level of classical computers has made the criteria for achieving quantum supremacy clear, making it easier for us to set future goals. With the target now clearer, it is expected that this development will encourage further progress of quantum algorithms.

Journal Information
Publication: Science
Title: Variational benchmarks for quantum many-body problems
DOI: 10.1126/science.adg9774