The shapes of organisms are geometrically determined structures not dependent on genes ― Discovery by Kanazawa University and others

Most insects have compound eyes, which are made up of small, hexagonal lenses closely packed together; these lenses are known as 'facets'. But why are they hexagonal? Thinking about it, bee nests are also made up of a mass of hexagonal holes. When researchers explored the mystery of this shape woven by the natural world, they found through experiments involving the eyes of flies that it is a geometrically determined structure formed via two simple forces. This was clarified by a research group from Kanazawa University and other institutions, who say that this is interesting in a way unconnected to genetics.

From hexagons to squares...but why?

Looking at everyday life, squares are relatively noticeable when it comes to patterns covered with the same shape - for example, bathroom tiles, concrete block walls and board game grids. Conversely, in the world of animals, there are lots of hexagons, as mentioned at the start of this article. Researchers believed this is because, as the total length of the six sides is short and the structure is strong, this shape has the physical stability to robustly fill a space at a low cost.

However, shrimp and lobster eyes have square facets, and the Japanese mantis shrimp (Oratosquilla oratoria) has a mix of squares and hexagons. Flies' eyes are normally hexagonal, but there are square variants, and so it seems that this shape is not determined by physical stability alone. So, what mechanisms actually determine this shape?

Professor Makoto Sato, who studies developmental and mathematical biology at the Institute for Frontier Science Initiative, Kanazawa University, is driving research that combines biology and math, commented, 'There was a vague belief that hexagons were naturally selected due to physical laws, but there are cases that contradict this (like squares). There wasn't any research investigating this, and we wanted to clarify it.'

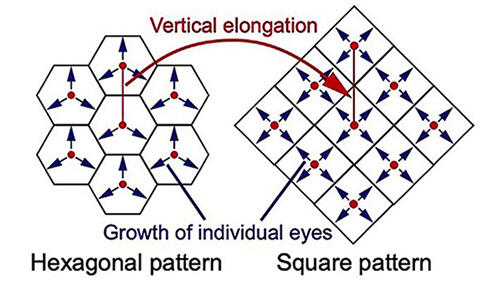
Thus, a research group made up of Professor Sato and his colleagues took on the challenge of verification using the eyes of Drosophila (fruit flies), which are often utilized as a model organism. First, they compared the variants with square facets to normal flies, taking note of the fact that the vertical height of their compound eyes was narrower. Perhaps the facets had deformed due to this shape? With this in mind, the group carried out an experiment by impinging a laser on the cell membranes of the variant and found that the compound eye was stretched on the vertical axis. As the vertical height of the compound eye was reduced, it was stretched by the surrounding area, and the facets that make up the compound eye were also stretched along with this.

However, it didn't seem possible that just being stretched would cause hexagons to become longer vertically and simply form tetragons. The research group actually continued their verification calculations from the perspective of physical stability for two years, but were completely unsuccessful. They could not obtain a conclusion that allowed for the tetragons.

The same mechanism that's used for assigning school districts!?

As the group felt an ever-stronger feeling of stalemate, one researcher had a flash of inspiration.

'Isn't this a Voronoi tessellation?'

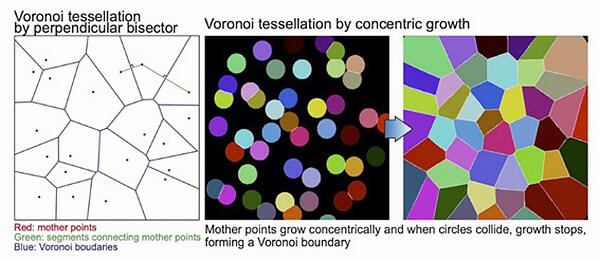
Voronoi tessellation is a method of evenly tessellating an area centered on multiple points on the surface. That sounds complicated, but it's easier to understand as an approach suited to deciding school districts for public elementary and junior high schools. The idea is that children commute to the nearest school, wherever their home is located. Thus, the perpendicular bisectors of the line segments connecting the schools (the points) to each other become the boundaries of the school districts. In the real world, factors such as administrative divisions, topography and school capacity are also involved in these boundaries, but this is just theoretical. Voronoi was the name of the mathematician who discovered this principle.

Having listened to that voice of inspiration, Professor Sato was initially skeptical: 'Voronoi tessellation simply means creating even tessellations with a ruler and a pencil. I don't think that explains anything.' However, when he carried out calculations based on this idea, they clearly explained the shape of the facets.

Of course, the shape of the facets of the flies' eyes is not determined by drawing perpendicular bisectors. But in the world of geometry, it is known that Voronoi tessellation is also possible in cases in which concentric circles grow from multiple points, like expanding balloons, and boundaries are formed as the circles collide with each other and the growth stops.

Thus, the group observed the eyes of Drosophila pupae as they grew, and ran a computer simulation. The results confirmed that the cells that form the facets really do expand like balloons, and so create an effect similar to Voronoi tessellation. The group was able to accurately explain not only the normal hexagons but also the variant tetragons using Voronoi tessellation. It is thought that something similar to the concentric circle growth from points in the world of geometry occurs in the facets.

According to conventional thinking, simple stretching creates a vertically long hexagon. This is not the case; the group have ascertained that Voronoi tessellation shapes are formed through the two forces of stretching and pushing outward, like an expanding balloon. It was already known that the shapes of the cells and tissues of living organisms are determined by genetic activity and physical constraints. This study has clarified that, in addition to these, geometric tessellation mechanisms also exist.

The research group was made up of researchers from Kanazawa University, Hokkaido University, the University of Toyama and Salesian Polytechnic. Their results were published in the electronic version of Current Biology, an American biology journal, on April 6, and announced by Kanazawa University, etc. on the 7th. The research was supported by the Japan Science and Technology Agency (JST) Strategic Basic Research Programs, Grants-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science and Technology, Grants-in-Aid for Scientific Research from the Japan Society for the Promotion of Science, the Network Joint Research Center for Materials and Devices, the Takeda Science Foundation, the Uehara Memorial Foundation and others.

Now that it is finally solved... something even elementary school students can understand

'A lot of recent papers on biology have involved genetics and molecules and been hard to understand. But this outcome involves absolutely no genes, and we were able to explain it completely through two simple forces. Even elementary school students can probably comprehend it, but biologists and mathematicians came together to finally solve it. That was also interesting, and has a sense of charm,' said Professor Sato.

The results of this research concern Drosophila, but this geometric tessellation mechanism may also be present in other organisms. In addition to the compound eyes of other organisms, Professor Sato has raised the specific examples of the arrangement of the seeds in a sunflower, the tips of field horsetail spore stems, and the geometric patterns seen on the shells of turtles/tortoises and armadillos. There are also columnar structures in the brain, made up of a regular assembly of neurons, and he notes that the liver consists of hexagonal hepatic lobules, which are collections of large numbers of cells.

Even if these shapes are known, the mechanisms that form them have been the subject of very few studies. 'We have a new research path: to confirm whether the mechanism we have found in this study can be applied in other cases. As these are living organisms, it would not be strange at all if the same mechanism did exist.'

Professor Sato and his colleagues will be carrying out more detailed research on compound eyes, and also investigating the neural cell columnar structures. 'Even if this research isn't directly useful for anything, it's interesting.' Even if it yields a basic science result, there is a possibility that it can be applied to bioengineering research in the future, such as artificial tissues and artificial organs.

As I heard the Professor speak, I suddenly recalled Romanesco, an imported vegetable in Japan. Romanesco is similar to broccoli and cauliflower, but has strange geometric patterns that make it resemble a piece of art. These have been added by human hands through selective breeding and similar methods, but it would be interesting to learn math from the natural world and living organisms.